myStudy [matheomnibus] [Plan und Konzept] [Themen] [Werkzeuge]
www.mathematik-sehen-und-verstehen.de
|
www.leuphana.de/matheomnibus
myStudy [matheomnibus] [Plan und Konzept] [Themen] [Werkzeuge] |
www.mathematik-sehen-und-verstehen.de |
| ||
| Graphentheorie |
| Ausführlicher Text in meinem Buch "Mathematik sehen und verstehen", Kapitel 3 | Vorlesung 1 2015 am 1. Tag |
 |
Die Aufgaben und Lösungen stehen in myStudy |
||||||
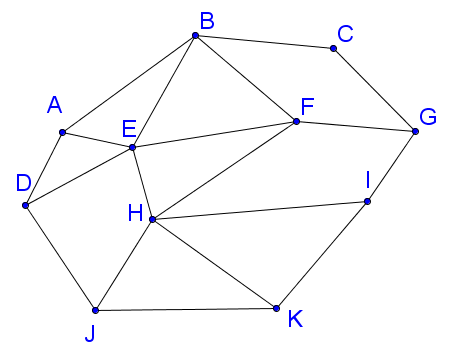 Ein Graph ohne Kreiswege heißt Baum. Ein Spannbaum ist ein Baum, der "den Graphen aufspannt", der also zusammenhängend ist und alle Knoten enthält. Als Länge eines Weges (in eimem ungewichteten Graphen) wird die Zahl der in ihm enthaltenen Kanten genommen. | |||||||
| Bei "gewichteten Graphen" sind den Kanten Gewichte zugeordnet. Bei schlichten Graphen (d.h. ohne Doppelkanten) können diese auch in der Adjazenzmatrix angegeben werden. Nun wird als Weglänge die Summe der Kantengewichte genommen. | |||||||
| Aufgaben zu Bäumen |
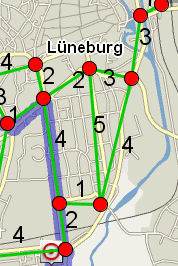
Minimale Spannbäume. Aufgabe zum Minimalen Spannbaum Lösung der Aufgabe zum Minimalen Spannbaum Bei Färbungen steht eine weitere Aufgabe. Kürzeste-Wege-Bäume Problem: Bestimme von einem Startknoten aus die kürzesten Wege zu allen Knoten des Graphen Aufgabe zum Routenplan Lösung der Aufgabe zum Routenplan  http://www-m9.ma.tum.de/Allgemeines/DijkstraApplet der TU München
Dijkstra-Algorithmus (nur für Spezialisten, nicht mfa)  
in etwas gewandelter Schreibtechnik.
| ||||||
| Färbungsprobleme | Eckenfärbung | ||||||
| Konfliktgraph | Aufgabe zu Konfliktgraphen im Zoo Lösung der Aufgabe zu Konfliktgraphen im Zoo Aufgabe Minimaler Spannbaum und Landkarte Lösung zur Aufgabe Minimaler Spannbaum und Landkarte  |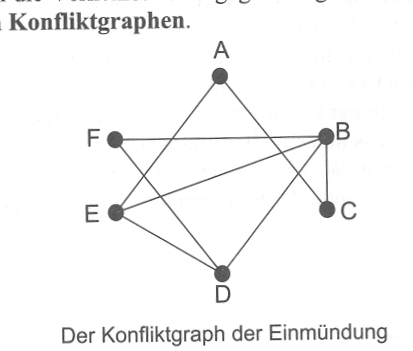
|
| ||||
