www.leuphana.de/matheomnibus     myStudy
[matheomnibus]  [Plan und Konzept]  [Themen]  [Werkzeuge] 

www.mathematik-sehen-und-verstehen.de
© Prof. Dr. Dörte Haftendorn 
noch mehr Moderne Mathematik
Ausführlicher Text in meinem Buch "Mathematik sehen und verstehen", Kapitel 5Vorlesung keine 2015 eingestreut
Kryptografie  Codierung  Graphentheorie 
Diese drei Bereiche der Diskreten Mathematik haben nun eigene Leitseiten.

Knotentheorie
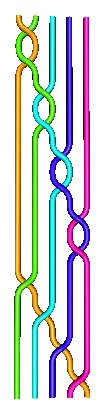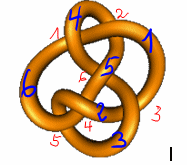
Die Knotentheorie versucht, Knoten zu klassifizierien, festzustellen, ob Entwirrbarkeit möglich ist, den Aufbau von Zöpfen zu beschreiben und vieles mehr.
Diese Methoden sind von der Genforschung, von der "Stringtheorie" der Physik und anderen Wissenschaften aufgegriffen worden.

Fraktale
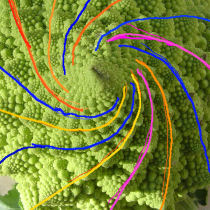Fraktale erhält man aus sehr einfachen Grundideen. Sie haben dennoch eine fein verästelte Struktur. Wenn man die fraktale Dimension von "verästelten" Stukturen der Natur kennt, dann kann man mehr über sie vorhersagen. Beispiele sind Korallenriffe, Wolkenbildungen, Schwämme, Bronchien....
In der Natur kommen auch die Aspekte der "Selbstähnlichkeit" und "Skaleninvarianz" reichhaltig vor.

Chaos und Mandelbrotmengen
Es ist das Verdienst der Chaostheorie, im allgemeinen Wissenschaftsbewusstsein verankert zu haben, welche tiefgründige und unüberschaubare Natur schon einfachen Gesetzen haben. Bei der Formel, die für die beiden oberen Zeichnungen verantwortlich ist, wird lediglich immer wieder eine Zahl quadriert und zum Ergebnis eine feste Zahl addiert.
[matheomnibus]  [Themen]   [Werkzeuge]        myStudy
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Okt 2007, update 6. Okt 2015

 www.leuphana.de/matheomnibus       www.mathematik-verstehen.de
www.doerte-haftendorn.de     www.kurven-erkunden-und-verstehen.de
www.mathematik-sehen-und-verstehen.de