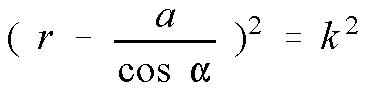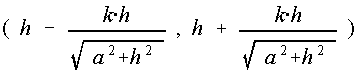Archiv: Diese Seiten werden nicht mehr direkt bearbeitet!

Zum Thema Kurven habe ich 2017 ein grundlegendes Buch "Kurven erkunden und verstehen" geschrieben.
Daher finden Sie sehr viel in www.kurven-erkunden-und-verstehen.de und Kurven bei Mathematik-Verstehen
Dort findet Pflege und Weiterführung dieser Themen statt.
Seit 2004 hat sich das weltweit frei verfügbare umfassende dynamische Mathematiksystem GeoGebra durchgesetzt.Es ist in allen meinen Büchern und Sites eingesetzt.

	Johanneum zur EXPO 2000	Johanneum 1998
	Die Natur als Erfindung des Menschen
	Mathematik als Erfindung des Menschen

Hundekurve oder Konchoide des Nikomedes

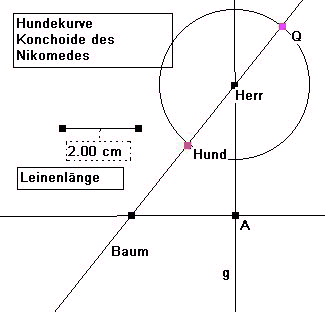Konstruktionsbeschreibung:

Zeichne eine Gerade g, die Straße, auf der der Punkt Herr sich bewegen kann.
Setze einen Punkt Baum irgendwo neben die Gerade g.
Diese beiden Punkte müssen jetzt miteinander verbunden werden.
Lege eine Strecke mit der Leinenlänge fest. Um den freien Punkt Herr zieht man nun einen Kreis mit der Leinenlänge als Radius. Zunächst wählt man die Leinenlänge nicht zu groß.
Die Schnittpunkte des Kreises und der Geraden HerrBaum sind Punkte Hund und Q.
Die Hundekurve ist dann sie Ortskurve des Hundes, bzw. von Q, wenn der Herr auf der Straße g spazieren geht und der Hund an seiner festen Leine immer auf den Baum zustrebt.
Durch Veränderung der Leinenlänge erhält man weitere mögliche Formen der Hundekurve.

Geschichte

Die Hundekurve heißt auch Konchoide oder Muschelkurve des Nikomedes

Nikomedes war ein griechischer Mathematiker des 2. Jahrhunderts vor Christi.
Er benutzte die Konchoide, um berühmte geometrische Probleme der Antike zu lösen.

Beim Delische Problem soll aus einer gegebenen Würfelkante die Würfelkanten eines Würfels mit doppelt so großen Würfels konstruiert werden. Dazu wird eine passende Gerade konstruiert, die dann die Konchoide schneidet. Das ist dann zwar eine „exakte“ Konstruktion, aber sie ist nicht allein mit Zirkel und Lineal ausführbar. Die Mathematiker haben inzwischen bewiesen, daß man mit Zirkel und Lineal allein den Würfel nicht verdoppeln kann. (Lit: Weth, Schupp )

Auch die Dreiteilung eines Winkels ist ein solches nicht mit Zirkel und Lineal lösbares Problem. Nikomedes verwendete auch hierfür in ähnlicher Art die Konchoide.

Dieses Problem kann man aber auch mit der Trisektrix lösen, die extra danach ihren Namen bekommen hat.

Die Gerade G heißt Leitgerade. Man kann auch andere Leitkurven nehmen.
Nimmt man einen Kreis, erhält man Pascalsche Schnecken und die Kardioide.

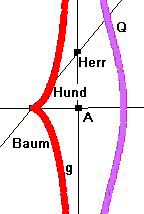
Die Formen der Konchoiden oder Hundekurven

Wenn die Leine genau von der Straße zum Baum reicht, hat die Hundekurve eine Spitze.
Wenn die Leine nicht von der Straße zum Baum reicht, hat die Hundekurve nur einen Bogen.
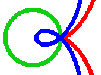
Wenn die Leine weiter reicht als von der Straße zum Baum, hat die Hundekurve eine Schleife.
Die violetten Äste der Hundekurve entstehen, wenn der Hund vom Baum wegstrebt anstatt zu ihm hin. Auf dieser Seite gfibt es nur eine typische Form.
Alle Konchoiden (Hundekurven) sind symmetrisch.
Ihre beiden Äste nähern sich der Straße an ohne sie zu erreichen. Die Gerade x=a ist Asymptote.

Formeln

Wenn das Zentrum im Baum ist, der Abstand Baum-Straße a und die Leinenlänge k ist gilt:

Gleichung in rechtwinkligen Koordinaten
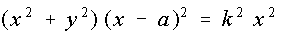Dieses ist eine algebraische Gleichung 4. Grades, weil x und y nur in Summen und Produkten vorkommen und der höchste Exponent (nach dem Klammerauflösen) 4 ist. Darum sind die Konchoiden algebraische Kurven 4. Grades.

Gleichung in Polarkoordinaten,

, oder griffiger:

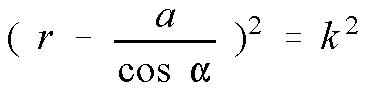
Gleichung der Kurvenpunkte in Parameterdarstellung. h ist der Abstand des Herrn von der x-Achse.

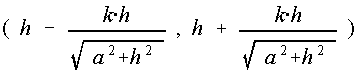
Autoren Klasse 8aL , Malte Bading, Web: [Dr. Dörte Haftendorn] Frühjahr 1998, letzte Änderung am 08. August 2023
[Exposystem] [Mathematik als Erfindung] [Mathematik 2000]