Archiv: Diese Seiten werden nicht mehr direkt bearbeitet!
 | Zum Thema Kurven habe ich 2017 ein grundlegendes Buch "Kurven erkunden und verstehen" geschrieben.
Daher finden Sie sehr viel in www.kurven-erkunden-und-verstehen.de und
Kurven bei Mathematik-Verstehen
Dort findet Pflege und Weiterführung dieser Themen statt.
Seit 2004 hat sich das weltweit frei verfügbare umfassende dynamische Mathematiksystem GeoGebra durchgesetzt.Es ist in allen meinen Büchern und Sites eingesetzt.
|

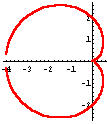 Kardioide, die Herzkurve
Kardioide, die Herzkurve
Geschichte
Ockham muss wohl in seine Teetasse geschaut haben, als er die
Kardioide 1691 in sein Lexikon der Mathematik aufnahm, denn dort (in
der Teetasse) kann man sie bewundern, sofern man gut genug hinschaut.
Man sollte auch wissen, dass es sich hier um eine halbe
Nephroide handelt. Den Namen Kardioide bekam die Kurve allerdings
von Cascillon 1741.
Nutzen:
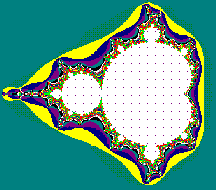
Eine Anwendung findet die Kardioide in der fraktalen Geometrie, denn sie
ist ein entscheidender Teil der Mandelbrotmenge oder (im Volksmund )
des Apfelmännchens. Eine kommerzielle Anwendung hat die
Kardioide allerdings nicht (wenn sie eine wissen sollten, können
sie uns ja schreiben!)
Wie sieht nun diese Kurve aus?
Eigentlich lässt sich dies anhand des Namens
sagen. Denn Kardioide heißt frei übersetzt
Herzkurve. Man kann sie in einer Kaffeetasse oder einem goldenen Fingerring beobachten, wenn helles Licht auf einen Punkt des Innenrandes fällt.
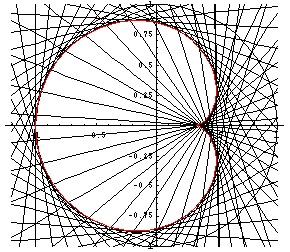
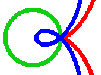
Im rechten Bild sieht man einen großen Kreis, den Tassenrand. Vom äußersten linken Punkt des Kreises gehen Lichtstrahlen aus, die aber nicht gezeichnet sind. Man kann sie nämlich auch in einer Kaffeetasse nicht sehen. Dafür sieht man aber die am Tassenrand reflektierten Strahlen. Sie sind hier (als Geraden) gezeichnet. Sie überlagern sich und hüllen eine Kurve ein, nämlich die Kardioide. Darum ist die Kardioide eine Katakaustik (Hüllkurve von reflektierten Strahlen).
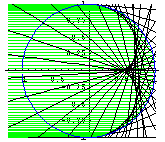 Fällt paralleles Licht, z.B. Sonnenlicht in die Tasse, so ist die entstehende Katakaustik eine Nephroide. (Schupp)
Fällt paralleles Licht, z.B. Sonnenlicht in die Tasse, so ist die entstehende Katakaustik eine Nephroide. (Schupp)
Wir haben mit der Hand viele Strahlen gezeichnet. Mit "Euklid" geht es nicht, weil man nur für Punkte und nicht für Geraden die Spur verfolgen kann.
Anmerkung: Allerdings kann man es mit dem Ti-92. Da kann man gut die Katakaustiken erkennen. Diese Bilder sind mit Mathematika gemacht. Das können wir noch nicht bedienen, weil man dazu mehr Mathematik können muss.
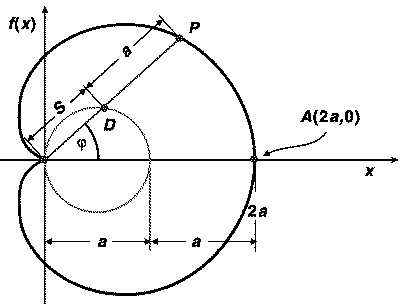 Wie lässt sie sich geometrisch konstruieren?
Wie lässt sie sich geometrisch konstruieren?
Das geht fast genauso wie bei der Hundekurve, nur die Straße ist nun ein Kreis durch den Baum. Die Leine ist doppelt so lang wie der Radius des Kreises. Die Deutung mit dem Hund klappt nicht so ganz, aber mathematisch entsteht wirklich die Kardioide.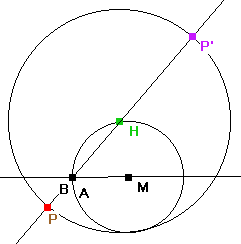
 Konstruktionsbeschreibung
Konstruktionsbeschreibung
Pascalsche Schnecken, Kardioide und noch andere Kurven
<- Zeichne an den Rand eine Strecke, die die Leinenlänge darstellt, und miss ihre Länge.
- Zeichne eine Gerade BM und auf ihr einen Punkt A.
- Zeichne um M einen Kreis durch A. Radius r=c/2.
- Setzte einen Punkt H auf den Kreis.
- Zeichne die Gerade HB.
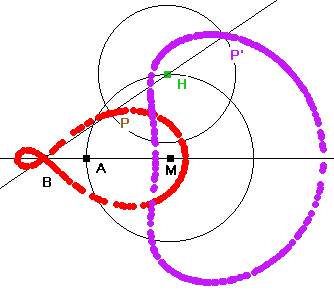
- Der Kreis um H mit der Leinenlänge aus 1) als Radius schneidet diese Gerade in P und P'.
- Gesucht ist der geometrische Ort von P und P', wenn H auf dem Kreis um M läuft.
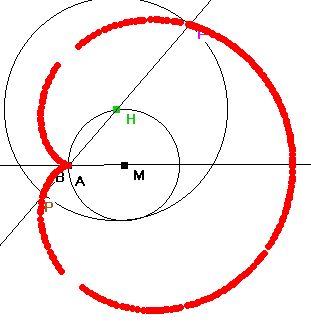
- Ziehe A auf B. Der Baum steht dann auf der "Kreisstraße".
in dieser Stellung erhält man alle Pascalschen Schnecken. (Bild rechts)
- Ziehe nun noch H auf die Gerade BM.
- Ziehe an der Leinenlänge, bis der Kreis um H auch durch B verläuft.
- In diesem Sonderfall ist die Ortskurve die Kardioide (oben dick rot, rechts blau)
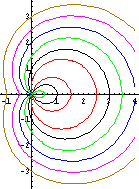
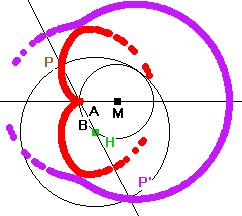
- Allerdings muss man links vom Ursprung den Punkt P und rechts den Punkt P' nehmen. Der jeweils andere Punkt läuft auf
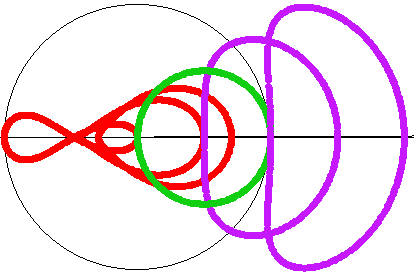
einem Kreis um den Ursprung mit dem Radius c, dem Duchmesser des "Straßenkreises". Beachtet man das nicht, so entsteht nachfolgendes Bild links oben. Im zweiten Bild ist dieser Kreis dünn und der "Straßenkreis" grün.
- Andere Pascalsche Schnecken entstehen, wenn a auf b liegt, bei anderen Leinenlängen oder bei anderen Straßenkreisradien.
Die allgemeinereren Fälle ergeben merkwürdige Kurven, die wir nicht mehr untersucht haben.
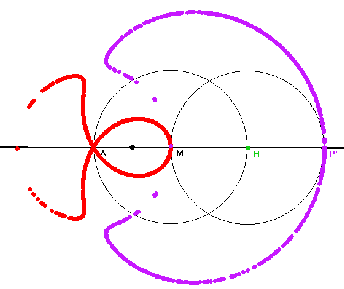
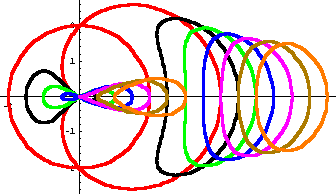 Liegt b nicht auf dem Straßenkeis, ergeben sich mit dem DGS Euklid und auch mit Mathematica zerfallende Kurven. Deren Namen haben wir nicht gefunden.
Liegt b nicht auf dem Straßenkeis, ergeben sich mit dem DGS Euklid und auch mit Mathematica zerfallende Kurven. Deren Namen haben wir nicht gefunden.
 Gleichungen für die Pascalschen Schnecken.
Gleichungen für die Pascalschen Schnecken.
Speziell mit 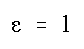 erhält man die Kardioide :
erhält man die Kardioide :
Sei BM die x-achse, auf der y-achse stehe B und c sei die Leinenlänge.
Der Baum B steht in A, also auf dem Straßenkreis.
Stets ist c epsilon = 2 R, dem Durchmesser des "Straßenkreises". Dann gilt:
Gleichung in rechtwinkligen Koordinaten
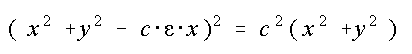 Dieses ist eine algebraische Gleichung 4. Grades, weil x und y nur in Summen und Produkten vorkommen und der höchste Exponent (nach dem Klammerauflösen) 4 ist. Darum sind die Kardioide und die anderen Pascalschen Schnecken algebraische Kurven 4. Grades.
Dieses ist eine algebraische Gleichung 4. Grades, weil x und y nur in Summen und Produkten vorkommen und der höchste Exponent (nach dem Klammerauflösen) 4 ist. Darum sind die Kardioide und die anderen Pascalschen Schnecken algebraische Kurven 4. Grades.
Gleichung in Polarkoordinaten,


Autoren Klasse 8aL Johannes Härke, Eike Petersen, Clemens Mädge, [Abi 2003] , Web: [Dr. Dörte Haftendorn] Frühjahr 1998, letzte Änderung am 08. August 2023
 [Exposystem] [Mathematik als Erfindung] [Mathematik 2000]
[Exposystem] [Mathematik als Erfindung] [Mathematik 2000]


 Kardioide, die Herzkurve
Kardioide, die Herzkurve
 Fällt paralleles Licht, z.B. Sonnenlicht in die Tasse, so ist die entstehende Katakaustik eine Nephroide. (
Fällt paralleles Licht, z.B. Sonnenlicht in die Tasse, so ist die entstehende Katakaustik eine Nephroide. ( Wie lässt sie sich geometrisch konstruieren?
Wie lässt sie sich geometrisch konstruieren?

 Konstruktionsbeschreibung
Konstruktionsbeschreibung




 Liegt b nicht auf dem Straßenkeis, ergeben sich mit dem DGS Euklid und auch mit Mathematica zerfallende Kurven. Deren Namen haben wir nicht gefunden.
Liegt b nicht auf dem Straßenkeis, ergeben sich mit dem DGS Euklid und auch mit Mathematica zerfallende Kurven. Deren Namen haben wir nicht gefunden.
 Gleichungen für die Pascalschen Schnecken.
Gleichungen für die Pascalschen Schnecken.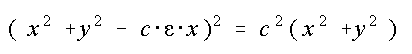 Dieses ist eine algebraische Gleichung 4. Grades, weil x und y nur in Summen und Produkten vorkommen und der höchste Exponent (nach dem Klammerauflösen) 4 ist. Darum sind die Kardioide und die anderen Pascalschen Schnecken algebraische Kurven 4. Grades.
Dieses ist eine algebraische Gleichung 4. Grades, weil x und y nur in Summen und Produkten vorkommen und der höchste Exponent (nach dem Klammerauflösen) 4 ist. Darum sind die Kardioide und die anderen Pascalschen Schnecken algebraische Kurven 4. Grades.