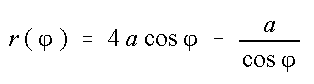Archiv: Diese Seiten werden nicht mehr direkt bearbeitet!
 | Zum Thema Kurven habe ich 2017 ein grundlegendes Buch "Kurven erkunden und verstehen" geschrieben.
Daher finden Sie sehr viel in www.kurven-erkunden-und-verstehen.de und
Kurven bei Mathematik-Verstehen
Dort findet Pflege und Weiterführung dieser Themen statt.
Seit 2004 hat sich das weltweit frei verfügbare umfassende dynamische Mathematiksystem GeoGebra durchgesetzt.Es ist in allen meinen Büchern und Sites eingesetzt.
|

Die Trisektrix
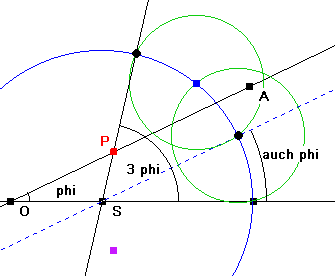
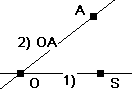 Konstruktionsbeschreibung der Trisektrix:
Konstruktionsbeschreibung der Trisektrix:
- Zeichne die Gerade OS.
- Wähle A beliebig und zeichne die Gerade OA.
- OA bildet mit OS den Winkel phi. Konstruiere eine Gerade g durch S, die mit OS den Winkel 3
phi bildet.
- OA und g schneiden sich in P.
- Die Trisektrix ist der geometrische Ort von P, wenn sich OA um O dreht.
 Die Geschichte:
Die Geschichte:
Wie die Cissoide und die Konchoide dient auch die Trisektrix zur Lösung eines "klassischen"
Problems der Geometrie, dem Dritteln des Winkels.
Im Laufe der Zeit beschäftigten sich viele Mathematiker und Laien damit, dieses Problem an
einem beliebigen Winkel mit Zirkel und Lineal zu lösen. Dass das nicht möglich ist, kann man
aber heute mit den Methoden der Algebra zeigen. Aber es gibt nichtelementare Lösungen, also
solche, die außer Zirkel und Lineal auch noch andere Hilfsmittel verwenden. Unter denen
befinden sich viele, die algebraische Kurven zu Hilfe nehmen.
Die bekannteste dieser Kurven ist die Trisektrix, die von Collin MacLaurin ( 1698-1746 )
erfunden wurde. Dieser Schotte wurde mit 19 Jahren Professor für Mathematik in Aberdeen
und ab 1726 in Edinburgh. Sein wichtigstes Werk "A treatise of fluxions" verfasste er 1746.
Die Konstruktion der Trisektrix von MacLaurin ist überraschend einfach.
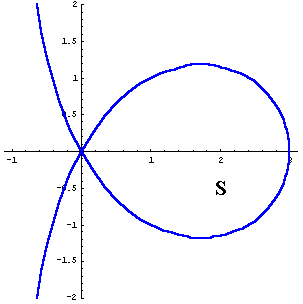 Winkeldritteln mit der Trisektrix:
Winkeldritteln mit der Trisektrix:
Hat man eine genaue Zeichnung einer Trisektrix (rechts im 1:1 Maßstab), so findet man S als Teilungspunkt 2:1 der
Strecke vom Kreuzungspunkt O zum Scheitelpunkt. Trägt man nun in S den Winkel an, den
man Dritteln will, so braucht man nur den Schnittpunkt des freien Schenkels mit der Trisektrix
mit O zu verbinden und erhält den Drittelwinkel.
Die mathematischen Formeln der Trisektrix
Der Ursprung des Koordinatensystems liege in O und der Abstand OS sei 2a.
Dann gilt die implizite Gleichung

Dieses ist eine algebraische Gleichung 3. Grades, weil x und y nur in Summen und Produkten vorkommen und der höchste Exponent (nach dem Klammerauflösen) 3 ist. Darum ist die Trisektrix eine algebraische Kurve 3. Grades.
Eine Parameterdarstellung ergibt sich unmittelbar aus dem Schnitt der beiden Geraden g1 und g2, indem man x eliminiert.
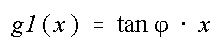 und
und
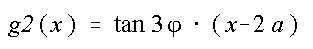
Eliminiert man aber mit Hilfe der trigonometrischen Formel
 den Winkel, so erhält man obige xy-Formel.
den Winkel, so erhält man obige xy-Formel.
Gleichung in Polarkoordinaten ist
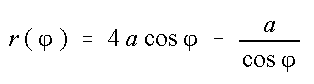
Besonderheit: Die Trisektrix geht bei Inversion an dem Kreis um den Scheitel durch O in sich
über. Darum gehört die Trisektrix zu den anallagmatischen Kurven.

Autoren Klasse 8aL Hauke Doerk , Web: [Dr. Dörte Haftendorn] Frühjahr 1998, letzte Änderung am 08. August 2023
 [Exposystem] [Mathematik als Erfindung] [Mathematik 2000]
[Exposystem] [Mathematik als Erfindung] [Mathematik 2000]


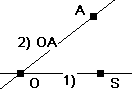 Konstruktionsbeschreibung der Trisektrix:
Konstruktionsbeschreibung der Trisektrix: Die Geschichte:
Die Geschichte: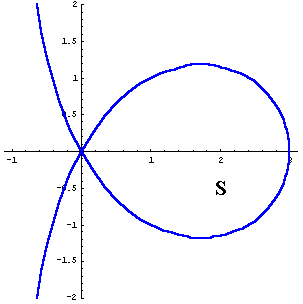 Winkeldritteln mit der Trisektrix:
Winkeldritteln mit der Trisektrix:
 den Winkel, so erhält man obige xy-Formel.
den Winkel, so erhält man obige xy-Formel.