Archiv: Diese Seiten werden nicht mehr direkt bearbeitet!
 | Zum Thema Kurven habe ich 2017 ein grundlegendes Buch "Kurven erkunden und verstehen" geschrieben.
Daher finden Sie sehr viel in www.kurven-erkunden-und-verstehen.de und
Kurven bei Mathematik-Verstehen
Dort findet Pflege und Weiterführung dieser Themen statt.
Seit 2004 hat sich das weltweit frei verfügbare umfassende dynamische Mathematiksystem GeoGebra durchgesetzt.Es ist in allen meinen Büchern und Sites eingesetzt.
|

Hyperbel
|
Definition
Die Hyperbel ist der geometrische Ort aller Punkte, die von zwei festen Punkten
F1 und F2, den Brennpunkten, eine konstante Abstandsdifferenz besitzen.
Die Hyperbel ist eine ebene Kurve, die zu den Kegelschnitten gehört.
|
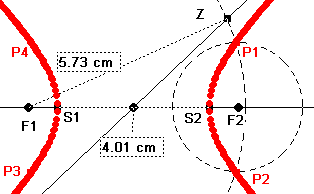
 Konstruktion Typ I Konstruktion Typ I
Zuerst werden die Brennpunkte F1 und F2 gesetzt, die durch eine Gerade verbunden
werden. Eine Abstandsdifferenz wird festgelegt (z.B L= 4,01 cm). Sie hat die Bedeutung des
Scheitelabstandes. Als nächstes wird um F1 ein Kreis mit beliebigen Radius geschlagen,
sein Radius r wird gemessen, r = 5,73cm. Um F2 wird ebenfalls ein Kreis geschlagen.. Sein
Radius muss so gewählt werden, daß die festgelegte Abstandsdifferenz entsteht. In
diesem Fall 1,62 cm, denn 5,73-r=4,01. Die Kreise schneiden sich in einem Punkt P.
Er und seine Spiegelpunkte bilden als Ortskurve die Hyperbel, wenn man r verändert.
Hier ist die Gerade, auf der Z nach außen gezogen wird "heimlich" als Asymptote
konstruiert, denn ein Kreis um O durch die Ecken des Rechtecks schneidet die x-Achse
in F1 und F2. Das Rechteck hat die Kanten 2a und 2b. Das passt zur Brennweiten-Formel der
Hyperbel:  |
 Hyperbelgleichung für die Mittelpunktslage mit
den Halbachsen a und b Hyperbelgleichung für die Mittelpunktslage mit
den Halbachsen a und b |
 In der Paramterdarstellung der Hypelbel stehen der
cosinus hyperbolicus und der sinus hyperbolicus, die wegen dieser Eigenschaft ihren Namen
bekommen haben. In der Paramterdarstellung der Hypelbel stehen der
cosinus hyperbolicus und der sinus hyperbolicus, die wegen dieser Eigenschaft ihren Namen
bekommen haben. |

mit 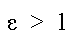 ist die
Polargleichung eines Astes. ist die
Polargleichung eines Astes. |
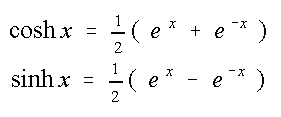 |
 Experimentierblätter
für die Arbeit von Hand
Experimentierblätter
für die Arbeit von Hand
Gezeichnet sind zwei "Kreiswellensysteme". Man kann nun Hyperbelpunkte durch
Abzählen erzeugen und farbig markieren. Man nimmt sich eine Differenz vor, z.B. 2 und
markiert die Schnittpunkte von Kreis 6 rechs und 4 links, dann 7 rechts mit 5 links, 8 mit
6 usw.
So entstehen die Hyperbelbögen.
In dieser Weise eignet sich das Blatt für eine Klassenarbeit nach dieser
Unterrichtsphase. Das Verfahren geht entsprechend auch für die Ellipse mit diesem Blatt.
Blatt in größer Darstellung als Vorlage (12K)
Anwendungen
Wenn man tatsächlich zwei "Kreiswellensysteme" auf einer
Wasseroberfläche erzeugt, so verstärken sich die Wellen, wo Berg auf Berg oder Tal auf
Tal trifft. Man nennt dieses Phänomen Interferenz, die Linien der
Verstärkung sind die Interferenz-Hyperbeln.
Interferenz tritt auch bei Schallwellen, bei Lichtwellen, Funkwellen u.a. auf. So dient
sie vielen Messvorgängen als Grundlage.
 Beim Spiegelteleskop wirken wirken die Kegelschnitte
in ihren Reflexionseigenschaften zusammen.
Beim Spiegelteleskop wirken wirken die Kegelschnitte
in ihren Reflexionseigenschaften zusammen.
Kühltürme und Silos haben Hyperbelquerschnitt, sie sind Rotationshyperboloide.
Das liegt vor allem daran, dass auf ihnen trotz der runden Form Geraden liegen. Daher kann
man sie aus Beton gut bauen.
Eine räumliche Fläche kombiniert aus Hyperbel und Parabel, das hyperbolische
Paraboloid, kommt im Straßenbau vor, wenn am Berg zwei Straßen
aufeinandertreffen und der Übergang "ausgerundet" werden muss.
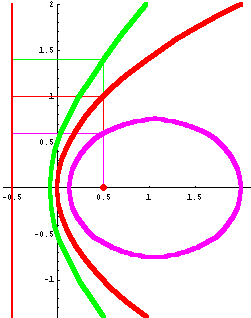
Auf Hyperbelbahnen fliegen Himmelskörper die nur vorübergehend in das
Schwerefeld eines Sternes oder einer großen Masse eintreten. Wenn sie von dem
Schwerefeld eingefangen werden, geht ihre Bahn in eine Ellipsenbahn über.
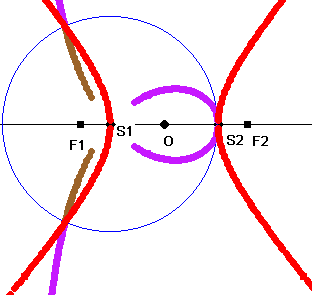 Auch innerhalb der Mathematik hat die Hyperbel große Bedeutung. Bei der Inversion am Kreis in der gezeichneten Lage geht die Hyperbel in
eine Strophoide über. So zeigt sich ein schöner Zusammenhang
zwischen den hier untersuchten Kurven.
Auch innerhalb der Mathematik hat die Hyperbel große Bedeutung. Bei der Inversion am Kreis in der gezeichneten Lage geht die Hyperbel in
eine Strophoide über. So zeigt sich ein schöner Zusammenhang
zwischen den hier untersuchten Kurven.
Geschichte
Ihre 2000 Jahre alte Geschichte teilt die Hyperbel mit den
andern Kegelschnitten.

Autoren Klasse 8aL , Web: [Dr. Dörte Haftendorn] Frühjahr 1998, letzte Änderung am 08. August 2023
 [Exposystem] [Mathematik als Erfindung] [Mathematik 2000]
[Exposystem] [Mathematik als Erfindung] [Mathematik 2000]


 Konstruktion Typ I
Konstruktion Typ I Hyperbelgleichung für die Mittelpunktslage mit
den Halbachsen a und b
Hyperbelgleichung für die Mittelpunktslage mit
den Halbachsen a und b In der Paramterdarstellung der Hypelbel stehen der
cosinus hyperbolicus und der sinus hyperbolicus, die wegen dieser Eigenschaft ihren Namen
bekommen haben.
In der Paramterdarstellung der Hypelbel stehen der
cosinus hyperbolicus und der sinus hyperbolicus, die wegen dieser Eigenschaft ihren Namen
bekommen haben.
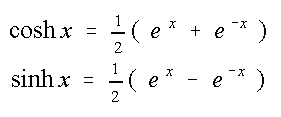

 Beim Spiegelteleskop wirken wirken die
Beim Spiegelteleskop wirken wirken die 
 Auch innerhalb der Mathematik hat die Hyperbel große Bedeutung. Bei der
Auch innerhalb der Mathematik hat die Hyperbel große Bedeutung. Bei der 