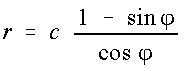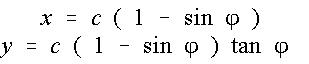Archiv: Diese Seiten werden nicht mehr direkt bearbeitet!
 | Zum Thema Kurven habe ich 2017 ein grundlegendes Buch "Kurven erkunden und verstehen" geschrieben.
Daher finden Sie sehr viel in www.kurven-erkunden-und-verstehen.de und
Kurven bei Mathematik-Verstehen
Dort findet Pflege und Weiterführung dieser Themen statt.
Seit 2004 hat sich das weltweit frei verfügbare umfassende dynamische Mathematiksystem GeoGebra durchgesetzt.Es ist in allen meinen Büchern und Sites eingesetzt.
|

Strophoide oder Seilkurve
Für die Strophoide haben wir drei Konstruktionen kennengelernt. Eine davon kam unter dem Namen Logocyklika in der Klassenarbeit dran.

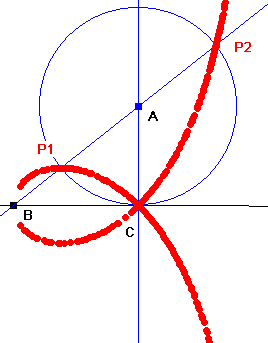 Konstruktion I
Konstruktion I
Auf BC ist in C die
Senkrechte g errichtet. Der Kreis um A auf g mit dem Radius AC
schneidet BA in P. Gesucht ist der geometrische Ort von P, wenn A auf
g wandert.
Bei dieser Konstruktion wird der Punkt B nie ganz erreicht.
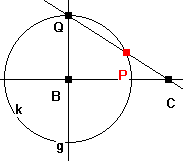
 Konstruktion II
Konstruktion II
Auf BC ist
in B die Senkrechte errichtet, Q liegt auf der Senkrechten. Der Kreis
um B mit dem Radius BQ schneidet QC in P.
Gesucht
ist der geometrische Ort von P, wenn Q auf h wandert.

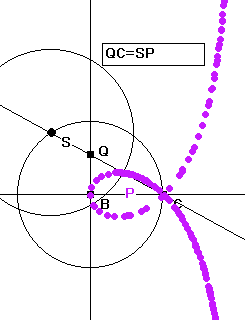 Konstruktion III (nach Weth)
Konstruktion III (nach Weth)
Auf BC ist
in B die Senkrechte h errichtet und um B ein Kreis mit dem Radius BC
geschlagen. Q liegt auf der Senkrechten. QC schneidet den Kreis in S.
Trägt man von S aus die Strecke QC auf der Geraden QC ab, so
entsteht P.
Gesucht
ist der geometrische Ort von P, wenn Q auf h wandert.
Gleichungen
für die Strophoide:
Wenn BC die x-Achse ist, die y-Achse in B steht und mit c die Strecke BC bezeichnet wird, gilt:
Gleichung in rechtwinkligen Koordinaten
 Dieses ist eine algebraische Gleichung 3. Grades, weil x und y nur in Summen und Produkten vorkommen und der höchste Exponent (nach dem Klammerauflösen) 3 ist. Darum ist die Strophoide eine algebraische Kurve 3. Grades.
Dieses ist eine algebraische Gleichung 3. Grades, weil x und y nur in Summen und Produkten vorkommen und der höchste Exponent (nach dem Klammerauflösen) 3 ist. Darum ist die Strophoide eine algebraische Kurve 3. Grades.
Gleichung in Polarkoordinaten,
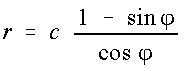
Gleichung der Kurvenpunkte in Parameterdarstellung mit dem Winkel der Polardarstellung
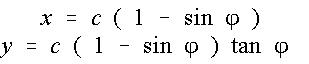
Geschichte
der Strophoide
In einem
Briefwechsel zwischen F. de Verdus und Torricelli von 1645 wird eine „Linie“ beschrieben, die
“...in Frankreich Ala oder Pteroide genannt wird...“. Die
Erfindung der Strophoide, wie die Kurve heute allgemein genannt wird,
geht somit auf einen französischen Mathematiker, wahrscheinlich
Roberval zurück. Eingeführt wurde dieser Name 1846 von Montucci.
Strophoide kommt aus dem Griechischen, stropho, und heißt Seil,
Band.
Sie hat aber noch viele andere Name, denn sie kommt vin vielen mathematischen Zuisanmmenhänge vor:
Ala, Pteroides torricellana, Fokale, Kukumaide, Logocyclica, harmonische Kurve.(nach Weth).

Autoren Klasse 8aL Friedemann und Lukas , Web: [Dr. Dörte Haftendorn] Frühjahr 1998, letzte Änderung am 08. August 2023
 [Exposystem] [Mathematik als Erfindung] [Mathematik 2000]
[Exposystem] [Mathematik als Erfindung] [Mathematik 2000]

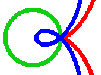

 Konstruktion I
Konstruktion I
 Konstruktion II
Konstruktion II 
 Konstruktion III (nach Weth)
Konstruktion III (nach Weth)