|
Vorlesung 14 (fertig)
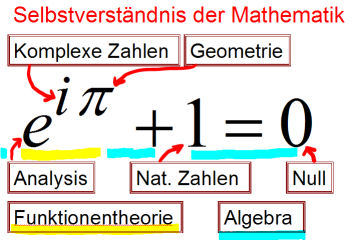
- Vorlesung 14 Selbstverständnis der Mathematik
 Handzettel Handzettel download download
- lecture 14: self-concept of mathematics
 handouts handouts download english download english
- Beweisen
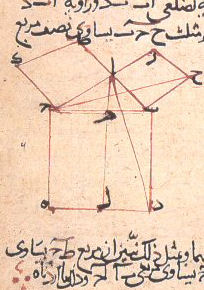
- Links ist der 2300 Jahre alte Beweis des Euklid zum Kathetensatz, aufgeschrieben in einem arabischen Buch.
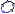 Euklids Beweis Euklids Beweis 
 Datei ohne den Text Datei ohne den Text  Winkelbegriff und Wechselwinkel an Parallelen Winkelbegriff und Wechselwinkel an Parallelen 
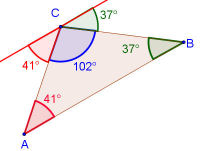
 - Darunter der Beweis des Winkelsummensatzes.
 Winkelsummensatz Winkelsummensatz 
 - In Mathematik beginnt der Aufbau einer "Theorie" mit Definitionen und Axiomen. Alle weiteren Aussagen dieser Theorie werden dann vollständig bewiesen. Wenn das Beweisen nicht gelingt, heiß die Aussage "Vermutung". Mathematische Theorien sind nicht wiederlegbar. Wenn jemand die Axiome anders festlegen möchte, wird entweder bewiesen, dass beide Axiomsysteme äquivalent sind oder man hat eben eine andere Theorie. Die kann aber nirgends der ersten Theorie widersprechen. Sie bezieht sich auf etwas Anderes.
 Stukturen suchen Stukturen suchen
- Rechts ist ein Beipiel aus dem Thema "Figurierte Zahlen" dargestellt. Es geht darum, wie sich die Anzahl der Karos entwickelt, wenn man immer weiter macht. In diesem Bereich werden viele Vorschläge schon ab der Grundschulmathematik gemacht.
- Die Algebra als mathematische Grundlagendisziplin beschäftigt sich ausdrücklich mit "algebraischen Stukuren". Diese haben Namen, die mit den Deutungen der Nichtmathematiker gar nichts zu tun haben: Halbgruppe, Gruppe, Halbring, Ring, Körper, Schiefkörper....
- Mathematiker gehen sauber und ordentlich mit dem Unendlichen um.
 Die harmonische Reihe divergiert. Die harmonische Reihe divergiert.
 - In Wissenschaft, Technik und Wirtschaft sind die Mathematiker vor allem wegen Ihrer Strukturierungs- und Generalisierungsfähigkeit gefragt.
|
|
 , allgemeines Vorgehen
, allgemeines Vorgehen