Archiv: Diese Seiten werden nicht mehr direkt bearbeitet!
 | Zum Thema Kurven habe ich 2017 ein grundlegendes Buch "Kurven erkunden und verstehen" geschrieben.
Daher finden Sie sehr viel in www.kurven-erkunden-und-verstehen.de und
Kurven bei Mathematik-Verstehen
Dort findet Pflege und Weiterführung dieser Themen statt.
Seit 2004 hat sich das weltweit frei verfügbare umfassende dynamische Mathematiksystem GeoGebra durchgesetzt.Es ist in allen meinen Büchern und Sites eingesetzt.
|

Parabel
 Definition
Definition
Die Parabel ist eine ebene Kurve, die zu den Kegelschnitten gehört. Bei der Parabel
hat jeder Punkt von einer festen Geraden, der Leitlinie g, denselben Abstand wie von einem
festen Punkt, dem Brennpunkt F.
Konstruktion
An Z wird eine Parallele zur Leitgeraden g nach außen gezogen. Der Abstand Zg wird als
Radius für einen Kreis um F verwendet. Die Schnittunkte P1 und P2 dieses Kreises mit der
Parallelen zu g durch Z sind die Parabelpunkte.
 Reflexionseigenschaft der Parabel
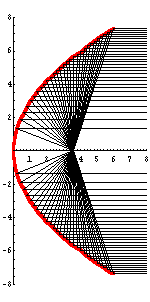
Reflexionseigenschaft der Parabel
Strahlen die von Brennpunkt ausgehen, werden achsenparallel reflektiert.
Achsenparallel einfallende Strahlen werden zum Brennpunkt reflektiert.
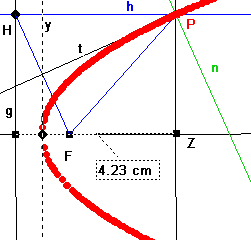
Nach Konstruktion ist HP=FP, t ist die Mittelsenkrechte im Dreieck HFP. Andere Punkte
von t sind von F und H gleichweit entfernt, also näher an g als an F. Kein anderer Punkt
auf t als P selbst kann also zu der Parabel gehören. Damit ist t Tangente an die Parabel.
n ist die Normale, die Senkrechte auf der Tangente. Die Winklel zwischen t und den blauen
Geraden durch P sind alle gleich groß. Damit sind auch die Winkel, die der
achsenparallele Strahl und der Brennpunktstrahl mit n bilden gleich groß. Also ist eine
Reflexion an P beschrieben, n ist das Einfallslot.
Alle Kegelschnitte haben höchst bemerkenswerte
Reflexioneigenschaften.
Übliche Formel für obige Lage:
Der Ursprung liegt im Scheitel. |
Übliche Formel im Schulunterricht mit der Parabelachse parallel zur
y-Achse |
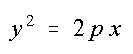 |
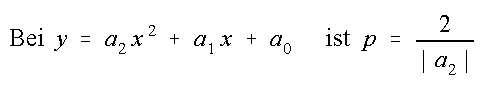 |
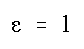 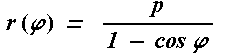 Die Gleichung oben links ist der Sonderfall der allgemeinen Kegelschnittgleichung für epsilon=1 Die Gleichung oben links ist der Sonderfall der allgemeinen Kegelschnittgleichung für epsilon=1
Entspechend ergibt sich die Gleichung in Polarkoordinaten.
Dabei liegt der Pol im Brennpunkt, die Parabel ist nach rechts geöffnet. |
Anwendungen
Wie oft die Parabel wird in unserem Alltag auftritt, wird uns meist nicht bewußt.
Zum Beispiel ist die Laufbahn beim Werfen eines Balles eine Parabel. Der Ball
fällt vom höchsten Punkt in einer Kurve derselben Form wieder zurück, wie er nach oben
geworfen wurde. Der Unterschied dabei ist aber, daß die Kurve gespiegelt ist. Beide
Bögen bilden die Parabel.
Auch bei Springbrunnen fliegen die Wassertropfen auf Parabelbahnen. Beim Feuerwerk sieht
man ganze Parabelfamilien
Die Reflexionseigenschaft der Parabel wird in vielen optischen
Geräten und bei Antennen ausgenutzt
Manche Gesetzmäßigkeiten in Natur und Technik können die "Parabelgesetze"
beschrieben werden.
Wenn ein Wasserglas rotiert, steigt das Wasser an den Rändern höher als innen, der
Querschnitt der Wasseroberfläche bildet eine Parabel. (gefunden bei Schupp)
Im Mathematikunterricht ist die Parabel als einfachste gebogene Kurve besonders
beliebt.

Autoren Klasse 8aL , Web: [Dr. Dörte Haftendorn] Frühjahr 1998, letzte Änderung am 08. August 2023
 [Exposystem] [Mathematik als Erfindung] [Mathematik 2000]
[Exposystem] [Mathematik als Erfindung] [Mathematik 2000]

 Definition
Definition
 Reflexionseigenschaft der Parabel
Reflexionseigenschaft der Parabel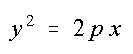
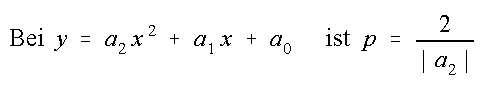
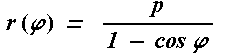 Die Gleichung oben links ist der Sonderfall der
Die Gleichung oben links ist der Sonderfall der 