Archiv: Diese Seiten werden nicht mehr direkt bearbeitet!
 | Zum Thema Kurven habe ich 2017 ein grundlegendes Buch "Kurven erkunden und verstehen" geschrieben.
Daher finden Sie sehr viel in www.kurven-erkunden-und-verstehen.de und
Kurven bei Mathematik-Verstehen
Dort findet Pflege und Weiterführung dieser Themen statt.
Seit 2004 hat sich das weltweit frei verfügbare umfassende dynamische Mathematiksystem GeoGebra durchgesetzt.Es ist in allen meinen Büchern und Sites eingesetzt.
|

Ellipse
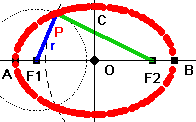 Definition
Definition
Die Ellipse ist eine ebene Kurve, die zu den Kegelschnitten gehört. Die Ellipse wird
von einem Punkt durchlaufen, dessen Abstände von zwei festen Punkten F1, F2 (den
Brennpunkten) eine konstante Summe besitzen.
Wir haben zuerst mit einem langen Band eine Ellipse an die Tafel gezeichnet.
Konstruktion Typ I
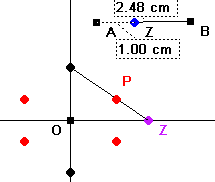
Zuerst werden die Brennpunkte F1 und F2 gesetzt, die durch eine Gerade verbunden
werden. Eine Abstandssummme wird festgelegt (z.B L=10 cm). Als nächstes wird um F1 ein
Kreis mit beliebigen Radius geschlagen, sein Radius r wird gemessen, r = 4 cm. Um F2 wird
ebenfalls ein Kreis geschlagen, der den Kreis um F1 "ergänzen" soll. Sein
Radius muss so gewählt werden, daß die festgelegte Abstandssumme entsteht. In diesem
Fall 6 cm, denn 10-r=10-4=6. Die Kreise schneiden sich in einem Punkt P. Er bildet als
Ortskurve die Ellipse, wenn man r verändert.
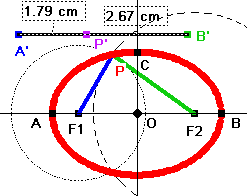 Konstruktion Typ II ohne Rechnung
Konstruktion Typ II ohne Rechnung
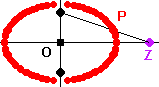
Man legt sich eine Strecke A'B', den Faden zurecht und setzt auf sie den Teilungspunkt
P'. Als Radien der Kreise um die Brennpunkte nimmt man nun die Abstände von P' zu den
Streckenenden. Zieht man an P', beschreibt P die Ellipse.
Verschiedene Formen erhält man durch verschiedene Fadenlängen. Auch die
Brennweite kann man verändern.
Insbesondere erhält man einen Kreis, wenn die Brennpunkte aufeinander liegen.

 Ellipsoid
Ellipsoid
Ein Ellipsoid ist ein geometrischer Körper. Das Rotations-Ellipsoid entsteht, wenn
eine Ellipse um eine ihrer beiden Achsen rotiert.
Die allgemeinste Form hat aber nur 3 Symetrieebenen; a große, b mittlere und c kleine
Halbachse.
 Anwendungen
Anwendungen
Seit der Zeit der Griechen wurde die Konstruktion der Ellipse zum Anlegen geometrischer
Gartenflächen benutzt. In den Schlossgärten aus der Barockzeit wurden Beete und
Rasenflächen geometrisch angelegt. In derselben Zeit sind auch Fenster in Ellipsenform
gebaut worden.
Eine Ellipse tritt auch auf, wenn man eine Wurst schräg anschneidet.
Mit der Ellipse als Kegelschnitt hängt direkt zusammen,
dass man mit dem Lichtkegel einer Taschenlampe an einer weißen Wand eine Ellipse erzeugen
kann.
Wenn man einen Kreis aus einer schrägen Blickrichtung ansieht, sieht man eigentlich eine
Ellipse. Nur wenn man weiß, dass es eigentlich ein Kreis ist, nimmt unser Gehirn das gar
nicht wahr.
Die Ellipse hat -wie auch auch die anderen Kegelschnitte- noch wichtige Reflexionseigenschaften
| Die drei Keplerschen Gesetze der
Planetenbewegung |
Das fand Johannes Kepler
(1571-1630) |
| Die Planetenbahnen sind Ellipsen, in deren einem
Brennpunkt die Sonne steht. |
Der Fahrstrahl Planet-Sonne überstreicht in gleichen Zeiten
gleiche Flächen. |
Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich zueinander
wie die dritten Potenzen der großen Halbachsen ihrer Bahnen. |

Autoren Klasse 8aL Maike, Harriert, Maria, Anna-Maria , Web: [Dr. Dörte Haftendorn] Frühjahr 1998, letzte Änderung am 08. August 2023
 [Exposystem] [Mathematik als Erfindung] [Mathematik 2000]
[Exposystem] [Mathematik als Erfindung] [Mathematik 2000]

 Definition
Definition Konstruktion Typ II ohne Rechnung
Konstruktion Typ II ohne Rechnung

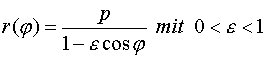


 Anwendungen
Anwendungen