Archiv: Diese Seiten werden nicht mehr direkt bearbeitet!
 | Zum Thema Kurven habe ich 2017 ein grundlegendes Buch "Kurven erkunden und verstehen" geschrieben.
Daher finden Sie sehr viel in www.kurven-erkunden-und-verstehen.de und
Kurven bei Mathematik-Verstehen
Dort findet Pflege und Weiterführung dieser Themen statt.
Seit 2004 hat sich das weltweit frei verfügbare umfassende dynamische Mathematiksystem GeoGebra durchgesetzt.Es ist in allen meinen Büchern und Sites eingesetzt.
|
Das Dreiblatt
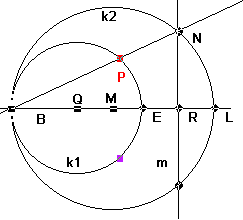Konstruktion:
- Zeichne ein Gerade g.Wähle auf ihr freie Punkte B,Q,M.
- Zeichne einen Kreis um Q durch B, er schneidet g in E.
- Zeichne einen Kreis um M durch B, er schneidet g in L.
- m ist die Mittelsenkrechte von EL,sie schneidet 3) in N.
- Zeichne die Gerade BN.
- BN schneidet 2) in P.
- Gesucht ist der geometrische Ort von P, wenn Q auf g wandert.
- Das ganze Dreiblatt entsteht, wenn auch der Spiegelpunkt von P an g betrachtet wird.
Geschichte
Die Kurve heißt "Gerades Dreiblatt". Nach Loria wurde sie von dem Franzosen G. de Longchamps gefunden, der sie "Trifolium droit" nannte. (zitiert nach Weth) Die Lebensdaten von Longchamps haben wir nicht gefunden. Die obige Konstruktion entspricht etwa der Aufgabe BERLIN aus dem Buch Anschauliche Analysis Bd. 2. Bei Schupp haben wir gelesen, dass das gerade Dreiblatt auch eine Fußpunktkurve einer besonderen Abrollkurve ist.
Formeln
Das Koordinatensystem steht bei B. Der Radius des großen Kreises ist 1.
Gleichung in rechtwinkligen Koordinaten:
Dieses ist eine algebraische Gleichung 4. Grades, weil x und y nur in Summen und Produkten vorkommen und der höchste Exponent 4 ist.. Darum ist das Dreiblatt eine algebraische Kurve 4. Grades.
Punkte des Dreiblattes in Parameterdarstellung, Radius a des kleinen Kreises als Parameter:
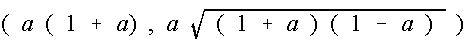
Autoren Klasse 8aL , Web: [Dr. Dörte Haftendorn] Frühjahr 1998, letzte Änderung am 08. August 2023
[Exposystem] [Mathematik als Erfindung] [Mathematik 2000]
