Archiv, diese Seiten werden nicht mehr aktualisiert.
Johanneum Lüneburg zur EXPO 2000 Dr. Dörte Haftendorn
Fraktale als Erfindung des Menschen		   unten
Mathematik als Erfindung des Menschen   Fraktale    Wegfraktale   Galerie der Wegfaktale     Mathematik 2000

Chaos und Fraktale jetzt neu vor allem bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg
Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten

Bäume

baump2 auf abbaum7
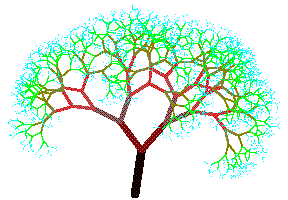baumm2 Meine schönsten Bäume habe ich in Mathematica entworfen. Mit diesem Werkzeug kann ich in besonderer Weise meine fein differenzierten Wünsche umsetzen. Man hat Zugriff auf die Ausgangsstellung, das Schmalerwerden, die Winkel, die Verkürzung und die Farben. Für die Farbübergänge habe ich mir Funktionen entworfen, die in den unterstehenden Realisierung in der Funktion zweigFarbe verborgen sind.

auf ab Realisierung in Mathematica

baumZF[stammVektor_,	zweigWinkelLinks_,stauchungLinks_,
			      	zweigWinkelRechts_,stauchungRechts_,
				stammDicke_,stauchungDicke_,
				iterationsTiefe_, options___]  :=
Module[{drehe,zweigZ, macheZweigeZ,alleZweigeZ},
	drehe[vec_,theta_]:={{Cos[theta],-Sin[theta]},{Sin[theta],Cos[theta]}}.vec;
	zweigZ[Line[{start_,ende_}]]:= {
	Line[{ende, ende+stauchungLinks
	drehe[ende-start,zweigWinkelLinks Random[Real,{0.5,1.5}]]}],
	Line[{ende,ende+stauchungRechts
	drehe[ende-start,zweigWinkelRechts Random[Real,{0.5,1.5}]]}] };
	zweigZ[Thickness[dicke_]] :=  Thickness [ stauchungDicke dicke] ;
	zweigZ[RGBColor[r_,g_,b_]] :=
		Module[ {},  zweigFarbe= RotateLeft[zweigFarbe];
		First[zweigFarbe]    ];
		macheZweigeZ[äste_]:=Flatten[ Map[ zweigZ,äste]];
	alleZweigeZ=NestList[ macheZweigeZ,{
		Thickness[ stammDicke], First[zweigFarbe],
		 Line[{{0,0},stammVektor}]},iterationsTiefe];
	Show[Graphics[alleZweigeZ ], options, AspectRatio->Automatic,PlotRange->All]
	]

auf ab Dimension

Die Baumfraktale sind zwar im weitesten Sinne selbstähnlich, aber nicht überschneidungsfrei, daher ist es nicht sinnvoll, die Selbstähnlichkeitsdimension auszurechnen.
nahSelbstähnlichkeitsdimension nahGalerie der Wegfraktale nahLeitseite Wegfraktale
Chaos und Fraktale jetzt neu vor allem bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg
Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten

Archiv, diese Seiten werden nicht mehr aktualisiert.
Autorin und Web: [Dr. Dörte Haftendorn] Email Frühjahr 2000, letzte Änderung am 09. August 2023
Exposystem [Exposystem] [Naturwissenschaften][Mathematik als Erfindung des Menschen][Mathematik 2000]