Prof. Dr. Dörte Haftendorn   [Kleine Schatztruhe]

Übungs-Klausur Mathematik II Name:

Prof. Dr. Dörte Haftendorn Universtität Lüneburg - Automatisierungstechnik

Gegeben ist die Differentialgleichung
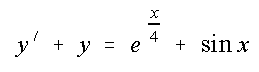
Mit dem Richtungsfeld
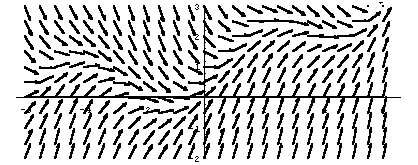
a) Es gilt die Anfangsbedingung

Bestimmen Sie mit der Schrittweite h=0,1

rechts neben dem Anfangspunkt P_o ( 0 / -1 ) näherungsweise noch zwei weitere Punkte P₁ und P₂ mit dem Heun-Verfahren.

Schreiben Sie hier nicht mehr als 4 wesentliche Dezimalen auf. Rechnen können Sie dennoch mit voller Anzeige. Notieren Sie Zwischenergebnisse nachvollziehbar.

b) Weisen Sie nach, dass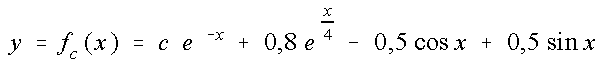 allgemeine Lösung der DGL ist.

c) Bestimmen Sie in f_c die Konstante durch Verwendung der Anfangsbedingungen aus a).

Berechnen Sie damit den Fehler, den Sie mit Ihrem 2. Punkt in a) gemacht haben.

d) Zeichen Sie die Lösung aus c) und zwei weitere deutlich verschiedene Lösungen grob ein.

Lösung Aufgabe 1

a) Skizzieren Sie die Funktion

aus zwei Bausteinen g und h . Nehmen Sie Stellung zum Gesamtverlauf.

b)Berechnen Sie die Nullstelle von f mit dem Newtonverfahren mit zwei Schritten. Notieren Sie Zwischenergebnisse nachvollziehbar.

c) Die Fläche unter f zwischen der Nullstelle und der Stelle x=0 rotiere um die x-Achse. Berechnen Sie das Volumen des entstehenden Rotationskörpers näherungsweise mit dem Keplerverfahren.

Lösung Aufgabe 2

a) Führen Sie den 1. Teil einer Laplacetransformation für die DGL durch.
Nur F(s) ist in gut weiterverwertbarer Form zu bestimmen.

b) Geben Sie den Ansatz für eine Partialbruchzerlegung des dabei auftretenden Terms
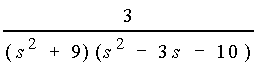
Deuten Sie an, wie nun ein Gleichungssystem entsteht.

Wählen Sie selbst frei erfundene Zahlen für die typischen Terme im Ergebnis und übersetzen Sie mit Hilfe der Tabelle zurück in den Originalbereich.
Die anderen Terme von F(s) brauchen Sie nicht zu berücksichtigen.

Lösung Aufgabe 3

Gemessen wurde (1 / 5) ; (2 / 8) ; (3 / 13) ; (4 / 22). Es handelt sich um eine Gesetzmäßigkeit des Typs

Bestimmen Sie a und b, indem Sie eine Ausgleichsgerade für die einfach-logarithmierten Daten errechnen. Eine Zeichnung ist nicht verlangt.

Lösung Aufgabe 4

Gegeben ist eine Kippschwingung ( siehe Bild).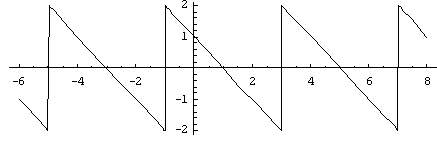

Bestimmen Sie mit Hilfe eines Tafelwerkes in nachvollziehbarer Form die Fourierentwicklung

Lösung Aufgabe 5