Gleitpunktzahlen dual nach IEEE-Standard
Mathematik mit MuPAD 2, Prof. Dr. Dörte Haftendorn 15.10.02 Version vom 15.10.02
----------------------------------------------------------------------------------------------------------------
Siehe auch Untersuchungen zur Maschinengenauigkeit und Zahldarstellung in Excel
Bin-Hex-Artithmetik in MuPAD
----------------------------------------------------------------------------------------------------------------
1 Bit Vorzeichen=S, 11 Bit Exponent=expo, 52 Bit Mantisse=F ohne führende1
0 100 0110 0010 001011...(52 Stellen).....0111000
Ein Wert ist dann für 0<expo<2047 gegeben durch
(-1)^S*2^(expo-1023)*1.F, der letzte Faktor in dualer Schreibweise,
d.h. dezimal, wenn man mit manti die dezimale Angabe von F bezeichnet
wert:=(-1)^S*2^(expo-1023)*(1+ manti/2^52)
Erstmal betrachten wir nur positive Werte, vorserstes Bit=0:
- wert:=2^(expo-1023)*(1+ manti/2^52)
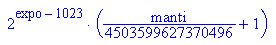
will man die sofortige Auswertung der Zweierpotenzen vermeiden,
muss man hold(...) verwenden.
Sonderfälle:(jeweils für beide S)
expo=2047, F> 0: wert:= NaN, Not a Number
0 111 1111 1111 001011...(52 Stellen).....0111000
expo=2047, F=0: wert:=infinity, unendlich
0 111 1111 1111 000000...(52 Stellen).....0000000
1 111 1111 1111 000000...(52 Stellen).....0000000
expo=0, F=0: wert:=0,
0 000 0000 0000 000000...(52 Stellen).....0000000
1 000 0000 0000 000000...(52 Stellen).....0000000
expo=0, F>0 : wertun:=(-1)^S*2^(1-1023)*manti/2^52 (unormalisiert)
0 000 0000 0000 001100...(52 Stellen).....1011100 z.B.
---------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------
Dieses ist festgelegt vom PSC (Pittsburgh Supercomputing Center)
http://www.psc.edu/general/software/packages/ieee/ieee.html
IEEE heißt Institut of Electrical and Electronic Engeneers
Dieser Standard gilt für unsere üblichen PC und viele andere,
nur wenige Großrechner haben andere Formate.
Man nennt diese Darstellung double precision,
64 Bit=8Byte-Darstellung
single precision arbeitet mit 1 Bit Vorz. 8 Bit Exponent, 23 Bit Mantisse
also einer 32-Bit(=4 Byte)-Darstellung
Eirweiterungen nach demselben Konzept sind gut denkbar.
- DIGITS := 25:S=0: k:=1023: m:=2^52:
Normalisierte Werte
- wert:=2^(expo-hold(k))*(1+manti/hold(m))
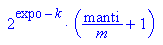
Unnormalisierte Werte
- wertun:=2^(1-hold(k))*(manti/hold(m))
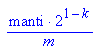
Einige Beispiele
Mit subs(term, x=3) wertet man einen Term für x=3 aus.
- subs(wert,expo=1026,manti=0)

0 000 0000 0010 00000...(52 Stellen).....0000
- subs(wert,expo=1023,manti=0)

- subs(wert,expo=1022,manti=0)
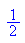
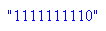
0 011 1111 1110 00000...(52 Stellen).....0000
- subs(wert,expo=1022,manti=2^51)
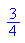
0 011 1111 1110 10000...(52 Stellen).....0000
Die kleinste Zahl in diesem Gleitpunktsystem darstellbare Zahl:
0 000 0000 0000 00000...(52 Stellen).....0001
1/20240225330731061835249534671891730704955664976414211835690135802743033956799534689196038370143712\
4495187077864316811911389808737385793476867013399940738509921517424276566361364466907742093216341239\
7676784727450685620074834246926986181033556491595563408100565123587695523334146152305025321863275086\
46006263307707741093494784
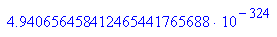
Kleinste Zahl der normalisierten Werte, das sind die mit Mantisse 1.F
0 000 0000 0001 00000...(52 Stellen).....0000
- subs(wert,manti=0,expo=1)
1/4494232837155789769323262976972561834044942447355766431835752028943316895137524078317711933060188\
400528002846996784833941469744220360415562321185765986853109444197335621637131907555490031152352986\
327073802125144220953767058561572036847827763520680929083762767114657455998681148461992907620883908\
2406056034304
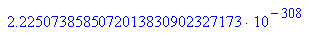
Das ist genau die in Excel beobachtete kleinste Zahl.
Daran sieht man, dass Excel die Erweiterung um die unnormalisierten Werte nicht verwendet.
Die größte Zahl, die noch nicht "unendlich" ist:
0 111 1111 1110 111111...(52 Stellen).....111111
- subs(wert,manti=2^52-1,expo=2^11-2)
179769313486231570814527423731704356798070567525844996598917476803157260780028538760589558632766878\
171540458953514382464234321326889464182768467546703537516986049910576551282076245490090389328944075\
868508455133942304583236903222948165808559332123348274797826204144723168738177180919299881250404026\
184124858368
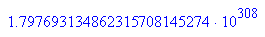
Maschinengenauigkeit eps=kleinste Zahl, deren Addition zu 1 von der Maschine gemerkt wird.
- (1+float(subs(wert,manti=0,expo=928))-1)
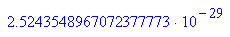
- (1+float(subs(wert,manti=2^52-1,expo=927))-1)

- (1+float(subs(wert,manti=2^52-1,expo=927))-1)

Damit ist klar, dass in MuPAD die Maschinengenauigkeit ist:
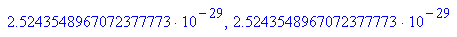
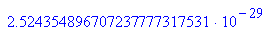

Also ist in MuPAD die Maschinengenauigkeit eps=2^(-95)
In Excel ist sie 2^(-49)
Internetadressen [www.doerte-haftendorn.de] [http://haftendorn.uni-lueneburg.de]
[http://haftendorn.uni-lueneburg.de/ing-math] [oben]


 [ing-math] [Numerik] Betreuung: Prof. Dr. Dörte Haftendorn
[ing-math] [Numerik] Betreuung: Prof. Dr. Dörte Haftendorn  , April 2002, update 19. Oktober 2002
, April 2002, update 19. Oktober 2002
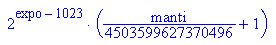
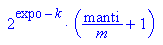
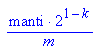

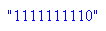
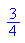
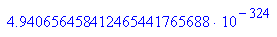
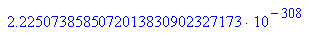


![]()
![]()
![]() [ing-math] [Numerik] Betreuung: Prof. Dr. Dörte Haftendorn
[ing-math] [Numerik] Betreuung: Prof. Dr. Dörte Haftendorn ![]() , April 2002, update
, April 2002, update