Archiv: Diese Seiten werden nicht mehr direkt bearbeitet!
Auf meiner Site www.mathematik-verstehen.de sind alle meine Themen angesprochen und weitergeführt. Vieles ist in meinen Büchern verständlich aufbereitet. Die Sites zu den Büchern www.mathematik-sehen-und-verstehen.de und www.kurven-erkunden-und-verstehen.de bieten die zugehörigen Geogebra-Dateien, Aufgabenlösungen und zusätzliche Informationen.
Seit 2004 hat sich das weltweit frei verfügbare umfassende dynamische Mathematiksystem GeoGebra durchgesetzt.Es ist in allen meinen Büchern und Sites eingesetzt.
Exposystem Johanneum zur EXPO 2000 Alphabetischer Index unten
Die Natur als Erfindung des Menschen
Mathematik als Erfindung des Menschen   

Platonische Körper

Die vollständig regelmäßigen Polyeder bezeichnet man als platonische Körper
Sie haben kongruente regelmäßige Seitenflächen und kongruente Ecken,
d.h. an jeder Ecke stoßen gleich viele dieser Flächen zusammen.
Das Wort "Polyeder" heißt "Vielflächner".

Didaktische und philosophische Anmerkung
Zahl der
Flächen,
die an einer Ecke
zusammen-
stoßen		Form der Seitenflächen,
es müssen regelmäßige Polygone sein
gleichseitiges
Dreieck		 Quadrat regel-
mäßiges
Fünfeck		 regel-
mäßiges
Sechseck
3
Mindestzahl
für eine
räumliche
Ecke
Tetraeder
Hexaeder
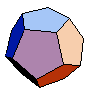Dodekaeder
4
Oktaaeder		 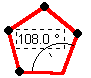4*108°  > 360°,
darum kann es keine weiteren
Körper mit vier Flächen
an einer Ecke geben.
5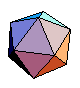
Ikosaaeder		 Vier Quadrate,
ebenso sechs gleichseitige Dreiecke und
drei regelmäßige Sechsecke,
die aneinanderliegen, bilden mit ihren Eckwinkeln einen Vollwinkel,
man kann keine keine räumliche Ecke erzeugen.
6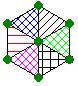
Bei seinen philosophischen Überlegungen zur Stuktur der Materie setze Platon (427- 348 v. Chr.) einen qualitätslosen Grundstoff voraus, dem die geometrischen Formen der regelmäßigen Körper aufgeprägt werden. Dabei kann man Feuer, Luft und Wasser, die alle mit Dreiecken aufgebaut sind, ineinander umwandeln, und zwar genau entsprechend der Anzahl der Dreiecke: zwei Teile Feuer ergeben ein Teil Luft, fünf Teile Luft ergeben 2 Teile Wasser. Aus Erde (Quadrat) kann hierbei kein Stoff anderer Art werden. Ebensowenig gilt das für das Dodekaeder , dieser "Gestalt bediente sich Gott für das Weltganze" [Timaios 53 c - 57 c] [Dieser Absatz aus: Gericke, Mathematik in Antike und Orient, Fourier, Wiesbaden 1992]
Körper
Namen Hexaeder
Sechsflächner
Würfel
Kubus		 Tetraeder
Vierflächner
regelmäßige Dreickspyramide		 Oktaeder
Achtflächner
regelmäßige
quadratissche Doppelpyramide		 Ikosaeder
20-Flächner		 Dodekaeder
12-Flächner
Platons Zuordnung Erde Feuer Luft Wasser Weltganzes

Der Mathematiker und Astronom Johannes Kepler hat am Beginn der Neuzeit um 1600 in seiner Vorstellung vom "mysterium cosmographicum" die platonischen Körper mit dem Planetensystem in Verbindung gebracht. Er sah darin einen Ausdruck göttlicher Vollkommenheit.

Didaktische und philosophische Anmerkung

Obige Überlegungen, dass es diese fünf und nicht mehr platonische Körper gibt, ist für mich eines der wunderbarsten elementaren Beipiele für die Kraft menschlichen Denkens. Darum nutze ich ab Klasse 6, wenn der Winkelbegriff gebildet ist, bis zu den ältesten meiner Schüler und Studenten jede Gelegenheit, diesen Gedanken zu fassen. Es ist ja nicht so, dass eben Platon diese fünf gefunden hat und vielleicht jemand einmal noch einige findet, sondern es kann nicht mehr davon geben. Und das wird nicht einer Autorität geglaubt oder nachgeplappert, sondern beruht dann auf jeweils eigener Einsicht der Lernenden.

Die platonischen Körper kommen in der Natur nur in angenäherter Gestalt vor. Mineralogie und Kristallografie klassifizieren mit "Idealgestalten", bei Ihnen sind aber andere Formen, z. B. Sechsecksäulen beim Basalt, genauso wichtig. Die platonischen Körper sind in diesem Sinne eine reine "Erfindung des Menschen".
Damit sind sie aber nicht einfach nur so "ausgedacht", sondern sie sind eine Wahrheit, die wir mit unserem menschlichen Geist erfassen können, jedenfalls ist dies mein Standpunkt in einer alten philosophischen Frage.


Autorin und Web: [Dr. Dörte Haftendorn] Email Frühjahr 2000, letzte Änderung am 09. August 2023
Exposystem [Exposystem] [Naturwissenschaften][Mathematik als Erfindung des Menschen][Mathematik 2000]