A:=matrix([[0.5,0.2,0.3],
[0.2,0.7,0.1],
[0.15,0.75,0.1]]);

Homogene Markowketten
Prof. Dr. Dörte Haftendorn MuPAD 4, Nov. 06 Nov. 08
http://www.mathematik-verstehen.de www.leuphana.de/matheomnibus
Achtung, am Ende der Datei sind A,v,s anders belegt! markstein-mfa.mn
################################################################################################
Wetter in Bad Markstein
Übergangswahrscheinlichkeiten: Sonne, Nebel, Regen
A:=matrix([[0.5,0.2,0.3],
[0.2,0.7,0.1],
[0.15,0.75,0.1]]);

A

A^2

A^3

Übergangsmatrix für das Wetter in Bad Markstein,
Zustände Sonne, Nebel, Regen
s:=matrix([[1,0,0]])
![]()
Startverteilung, Mathix kommt am Freitag bei Sonne an.
s*A
![]()
Wetterverteilung für Samstag, mit 50% W. ist Sa Sonne.
s*A*A
![]()
Wetterverteilung für Sonntag, mit 33,5% W. ist Sonntag Sonne.
Die Wetterverteilung der nächsten 3 Tage,
matrix([["Tag ".k,s*A^k] $k=0..5])

matrix([["Tag ".k,s*A^k] $k=0..20])

v:=s*A^20;v*A
![]()
![]()
Die Wetterverteilungen am 20. und 21. Tag unterscheideden sich gar nicht.
Das ist die stationäre Wetterverteilung von Bad Markstein.
Hier ist sie gefunden durch Potenzieren von A.
Bei dieser Wetterverteilung, herrscht einen Tag später dieselbe Wetterverteilung.
v*A
![]()
A^20

Betrachtet man A^20 selbst, so sieht man, dass der stationäre Verteilungsvektor
in allen Zeilen steht.
############################################################
M:=1/6*matrix([[2,3,1],[2,3,1],[2,3,1]]);
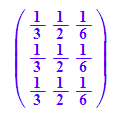
M^2
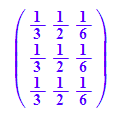
Stochastische Matrizen mit 3 gleichen Zeilen sind idempotent,
d.h. M^2=M
M:=1/(a1+a2+a3)*matrix([[a1,a2,a3],[a1,a2,a3],[a1,a2,a3]]);

simplify(M^2)

#####################################################################
Das Seniorenheim
A:=matrix([[0.1,0.5,0.4],
[0.2,0.8,0.0],
[0.40,0.20,0.40]]);

A

A^2

A^3

Übergangsmatrix für die Farben im Seniorenheim
s:=matrix([[0.5,0,0.5]])
![]()
Startverteilung, laut Aufgabenstellung
A

s*A
![]()
Farbverteilung nach einer Runde
s*A*A
![]()
Farbverteilung nach 2 Runden, mit 48% W. ist jemand "Grün".
Die Wetterverteilung der nächsten 3 Tage,
matrix([["Tag ".k,s*A^k] $k=0..5])

v:=s*A^20;
v*A
![]()
![]()
Die Farbverteilungen am 20. und 21. Tag unterscheiden sich gar nicht.
Das ist die stationäre Farbverteilung im Seniorenheim.
Hier ist sie gefunden durch Potenzieren von A.
(Eigenvektoren in anderer Markstein-Datei)