Dörte Haftendorn Lehrerfortbildung Multiplikatoren-Forum Doebler

Zur Hauptseite Dörte Haftendorn Zum alphabetischen Index

Subject:         Ergebnis der AG Stochastik (überarbeitet)
  Date:         Mon, 05 Oct 1998 18:41:40 +0200
  From:         Horst.Doebler@t-online.de (Horst Doebler)
    To:         	Reinhard Zimmer 
		Jürgen Stelling, 
		Gerhard Hillers
		Richard Hansen
		Dörte Haftendorn

Liebe Mitmultiplikator(inn)en,
ich habe unser Papier noch ein wenig korrigiert und grafisch aufgepeppt und schicke es erst einmal an Euch, die Ihr so einfach zu erreichen seid. Als doebstoc.doc
oder hier folgend in html
-- Bis dann, Grüße von Horst.
Horst.Doebler@T-Online.de
04167 / 911007

Lehrerfortbildung Betzendorf vom 28.9.-2.10.98

Arbeitsgruppe "Stochastik"

Thema: Bernoulli-Experimente und Binomialverteilung in Klasse 10

Vorkenntnisse: (Entspricht den RRL 7./8.Klasse)

Wahrscheinlichkeitsbegriff

Komplementärregel

relative Häufigkeit

Baumdiagramme

Pfadregeln

Grundkenntnisse im Umgang mit dem TI-92 (aus anderen Stoffgebieten)

1.Phase: (ca. 4 Stunden)

Ziel: Die Herleitung der allgemeinen Bernoulli-Formel

Hilfsmittel: Eingeführter Taschenrechner

Einstiegsaufgabe:

Eine Tüte Bananensamen enthält 6 Samen. Die Keimgarantie beträgt laut Tütenaufdruck 80%. Mit welcher Wahrscheinlichkeit keimen 0,1,2,3,4,5,6 Samen ?

Anhand dieser Aufgabe sollen folgende Aspekte erarbeitet werden:

Wahrscheinlichkeitsverteilung
Histogramm (ggf. Wiederholung aus der 7.Klasse)
Binomialkoeffizient

Bemerkung: Der Binomialkoeffizient kann eingeführt werden über:

das Pascalsche Dreieck
kombinatorische Überlegungen (bedingt 2 zusätzliche Stunden)

2.Phase: (ca. 3-4 Stunden)

Ziel: Berechnung und Darstellung von Binomialverteilungen mit Hilfe des TI-92

Erweiterung der Einstiegsaufgabe:

Mit welcher Wahrscheinlichkeit keimen von 90 Bananensamen genau 80% ?

Intendiertes Schülerverhalten:

Schätzen eines Ergebnisses
Genaue Berechnung mit dem TR

Die (erhoffte) Diskrepanz zwischen dem Schätzwert und dem berechneten Wert soll Anlaß sein, über diese Binomialverteilung zu diskutieren. Über den möglichen Zwischenschritt, mit dem TR weitere Einzelwahrscheinlichkeit zu berechnen, sollen die folgenden Ziele angestrebt werden:

Erstellen einer vollständigen Wertetabelle mit dem TI-92 (Data/Matrix-Editor)

Graphische Darstellung der Tabelle in einem Histogramm

Zu 1.: Befehlsfolge zur Eingabe in den Data/Matrix-Editor:

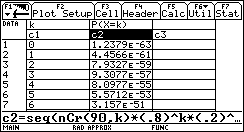
Apps/6/new/"Banane"(Eintrag unter "Variable") / Enter / Enter / c1=seq(k,k,0,90) / C2=seq(nCr(90,k)*0,8^k*0.2^(90-k),k,0,90) / Enter

Der Anfang der Wertetabelle sieht dann wie im Bild rechts aus:

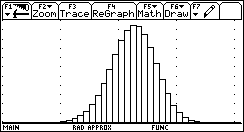
Zu 2.: Befehlsfolge zur Erstellung des Histogramms:

F2 (Plot Setup)/ freien Plot auswählen / F1 (Define) / Plot type: Histogram ; x: c1 ; Hist. Bucket Width: 1 (voreingestellter Standardwert) ; Use Freq. and Categories: Yes ; Freq: c2 / Enter

Für die globale Verteilung bei n=90 ist die Bildschirmauflösung zu gering. Deshalb sollte bei "WINDOW" z.B. der Bereich zwischen 50 und 91 für x eingestellt werden. Die Einstellung "grid on" unter F1 / 9:Format... gestattet ein Ablesen der Werte von P(X=k).

Anschließend:

Vertiefende Betrachtungen zu Binomialverteilungen durch die Variatiation der n- und p-Werte mit dem Ziel, Symmetrien der Histogramme zu entdecken und zu interpretieren. Dabei wird der Umgang mit dem TI-92 gefestigt.

3. Phase: (ca. 4 Stunden)

Ziel: Berechnung von Bereichswahrscheinlichkeiten

2.Erweiterung der o.a. Aufgabe:

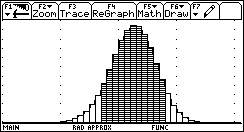
Wie groß ist die Wahrscheinlichkeit, daß man zwischen 67 und 77 Keimlinge erhält ?

Mögliche Lösungswege:

Addition der entsprechenden Werte mit dem TR

Addition innerhalb der Tabelle. (Hinweis: Festlegung des Tabellenbereichs von 67 bis 77 durch folgende geänderte und ergänzte Befehlsfolge (Änderungen und Ergänzung fett gedruckt): c1=seq(k,k,67,77) / C2=seq(nCr(90,k)*0,8^k*0.2^(90-k),k,67,77) / c3=cumSum(c2) / Enter

In Zeile 11 / Spalte c3 steht dann die Bereichswahrscheinlichkeit P(67£ X£ 77) » 0,854.

Alternative: Summationsbefehl 2nd / 4 in den man je eine Variable "untere" und "obere Grenze" einsetzen kann.

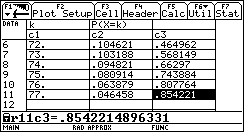
Weitere geeignete Übungsaufgaben sind den einschlägig bekannten Lehrbüchern zu entnehmen.

Begründung für den Einsatz des TI-92:

Verwendung realistischer Parameterwerte

Stochastik-Tabellen werden überflüssig

Schnelle Berechnung von Bereichswahrscheinlichkeiten

Darstellung und Interpretation von beliebigen Histogrammen

Weitere Hinweise für Lehrkräfte:

Die Berechnung der Tabelle ist bei großen n recht zeitintensiv. Man kann sie notfalls mit der "ON"-Taste abbrechen, die auf dem TI-92 eine BREAK-Funktion auslöst. In diesem Fall wird allerdings "Auto-Calculate" auf OFF gesetzt und muß bei der nächsten Berechnung unter F1 / 9:Format ... wieder auf ON gestellt werden.

Die Darstellung von Histogrammen mit großen n-Werten ist nicht möglich (Problem der Bildschirmauflösung)

Zum Schraffieren der Bereichswahrscheinlichkeit kann folgender Befehl verwendet werden: shade 0,b(n,p,int(x)),u,o,2 (Die letzte 2 kann durch 1,3, oder 4 ersetzt werden und legt die Schraffierungsart fest.)
u steht für die untere Grenze, o entsprechend für die obere Grenze. Funktionsdefinition im "Home-Editor": define b(n,p,k)=nCr(n,k)*p^k*(1-p)^(n-k)