Johanneum zur EXPO 2000
	Die Natur als Erfindung des Menschen
	Naturwissenschaften   Kristallphysik

"Modell und Wirklichkeit in der Physik, ein Beispiel aus der Kristallphysik", Bericht über einen Vortrag von Dr. Andreas Palmer, Berlin

Ausgleichskurven durch Messdaten

Wenn zwischen zwei physikalischen Größen ein Zusammenhang beobachtet wird, so gehört es zu den Aufgaben der Physik, die Gesetzmäßigkeit möglicht gut als mathematische Funktion zu beschreiben. Zunächt muss man sich -eventuell aufgrund theoretischer Überlegungen- für ein Modell entscheiden, das zu den beiden untersuchten Größen gehören könnte. Die Messdaten ergeben nie exakt eine "schöne" Kurve, sondern man sucht eine Modellkurve, die am besten zu den Messpunkten passt. Diese Kurve soll dann "Ausgleichskurve" heißen. Gauß hat mit seiner Methode der kleinsten Fehlerquadrate ein Kriterium, was "die beste Kurve" heißen soll, und eine Berechnungsmöglichkeit angegeben.	Gauß: Methode der kleinsten Fehlerquadrate Verbindet man die Messpunkte senkrecht mit der vorgeschlagenen Kurve und macht aus diesen Verbindungsstücken lauter Quadrate, dann ist die Ausgleichskurve diejenige Kurve (dieses Typs), bei der die Summe dieser Quadrate minimal ist.
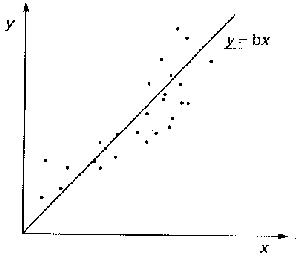
	Das einfachste Modell ist ein proportionaler Zusammenhang, dessen Graph ist eine Gerade durch den Ursprung. Man benötigt einen Parameter, die Steigung b.
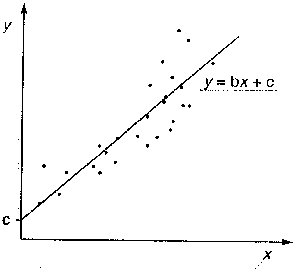
	Ein erweitertes Modell ist linearer Zusammenhang, d.h. eine Gerade, die nicht unbedingt durch den Ursprung verläuft. Man benötigt nun zwei Parameter, die Steigung b und den Achsenabschnitt c.
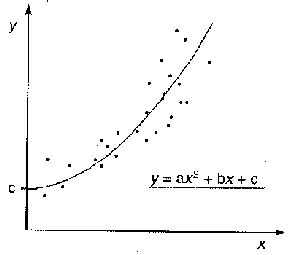
	Für ein Parabel-Modell (z.B. Wurfparabel) braucht man drei Parameter Wichtig sind noch Ausgleichskurven zu Exponentialfunktionen und beliebigen Potenzfunktionen. Zu ihrer Bestimmung nutzt man Ausgleichsgeraden der logarithmischen Darstellung.
Je höhere Anforderungen man an das Modell stellt, je besser man es an die vorliegenden Messungen und Erkenntnisse der physikalischen Zusammenhänge anpasst, desto mehr Parameter wird es (meist) geben. Bei der Untersuchung in der Kristallphysik, die hier beschrieben werden soll, waren es schließlich 30 Parameter.

Misst man eine physikalische Größe, so trifft man fast nie ihren wahren Wert, sondern allenfalls in seine Nähe. Allzuweit entfernt wird die Messung aber auch nur selten sein. Dieses drückt sich in der "Gaußschen Glockenkurve" aus. Auch wenn man dann einen Mittelwert aus allen Messungen ausrechnet, trifft man nicht unbedingt die Wahrheit. Mittelwerte "streuen" ebenfalls, nur nicht mehr so stark wie Einzelwerte. Ein Maß für die Streuung von Mittelwerten aus n Messungen ist , der "Standardfehler". Für sigma nimmt man (ersatzweise) die gemessene Standardabweichung s der Messreihe.
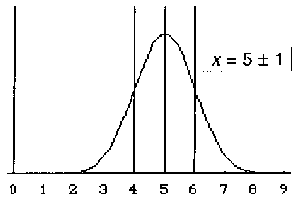
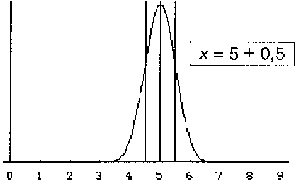
Das Intervall zwischen den beiden Wendestellen wird durch die Angabe Mittelwert beschrieben. Es wird von etwa 68% solcher Mittelwerte getroffen, ein doppelt so breites Intervall von gut 95%.	Der Standardfehler ist hier 0,5 und links 1. Da bei beiden Bildern der Mittelwert gleich - nämlich 5 - ist, gilt die Messung, die dem rechten Bild zugrunde liegt, als die bessere Messung. Die Physiker müssen darauf achten, dass die Standardfehler nicht so groß sind, dass sie den eigentlich zu messenden Effekt zudecken.

[Fragestellung und Versuchsaufbau] [Anpassung des Modells an die Messdaten] [Der NiF₂-Kristall] [Schlussfolgerung]

Autor: Dr. Andreas Palmer, Abitur 82 Web: [Dr. Dörte Haftendorn]  Datum: 29. Mai 99. Letzte Änderung am 19. Februar 2000
[Naturwissenschaften] [Kristallphysik] [Dokumentationsteam] [Email s.Ueberblick] [Informationssystem] [Physik]